Vector projection
Given two vectors \(\vec{A}\) and \(\vec{B}\), think of projecting \(\vec{A}\) onto \(\vec{B}\) as if \(\vec{A}\) was casting a shadow onto \(\vec{B}\), which is parallel to the ground. In the image below that would be the black vector on the bottom. Notice how it only goes as far as the light can project \(\vec{A}\) down-wards.
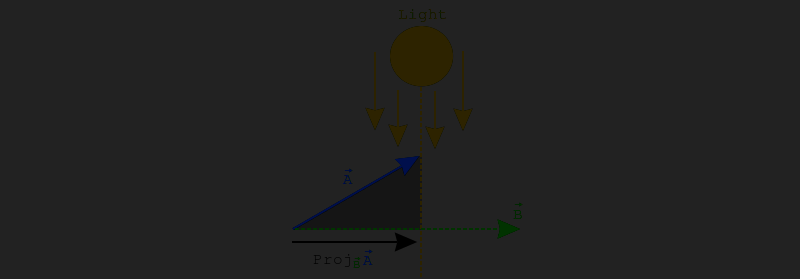
In the below demo, click and drag the green and blue vectors. The blue vector (\(\vec{A}\)) is being projected onto the green vector (\(\vec{B}\)). The projection vector appears in orange, while the rejection vector appears in red. The length of each vector is printed out in the upper right corner.
To project \(\vec{A}\) onto \(\vec{B}\), the direction of \(\vec{B}\), which is \(\hat{B}\) needs to be scaled by some scalar. This scalar is the component of \(\vec{A}\) in the direction of \(\vec{B}\). This component is a scalar value which can be found by dividing the dot product of \(\vec{A}\) and \(\vec{B}\) by the magnitude of \(\vec{B}\): \(comp_{\vec{B}}\vec{A} = \frac{\vec{A} \cdot \vec{B}}{\|B\|}\)
Once the component of \(\vec{A}\) in the direction of \(\vec{B}\) is found, it can be used to scale the normal of \(\vec{B}\): \(\hat{B} = \frac{\vec{B}}{\|B\|}\). This multiplication results in the final formula:
$$ proj_{\vec{B}}\vec{A} = \frac{\vec{A} \cdot \vec{B}}{\|B\|} \hat{B} = \frac{\vec{A} \cdot \vec{B}}{\|B\|^{2}} \vec{B} $$
Implementing this in code is trivial
// Project A onto B
vec Projection(vec a, vec b) {
float magBsq = MagnitudeSq(b);
assert(magBsq != 0);
float scale = Dot(a, b) / magBsq;
return Scale(b, s);
}
A slight optimization
Vectors are often projected onto normals. Assuming that \(\vec{B}\) is a normal vector, \(\hat{B}\), the value of \({\|B\|}\) would always be \(1\)! This simplifies the projection formula even further to just:
$$ proj_{\hat{B}}\vec{A} = (\vec{A} \cdot \hat{B})\hat{B} $$
Rejection
Projecting \(\vec{A}\) onto \(\vec{B}\) will yield a vector parallel to \(\vec{B}\). But, there is a parallel and perpendicular component of \(\vec{A}\) with respect to \(\vec{B}\). The perpendicular vector is called the rejection. Finding the rejection is simple, it's just the projection subtracted from the original vector:
$$ rej_{\vec{B}}\vec{A} = \vec{A} - proj_{\vec{B}}\vec{A} = \vec{A} - \frac{\vec{A} \cdot \vec{B}}{\|B\|^{2}} \vec{B} $$
Assuming that \(\vec{B}\) is normalized to \(\hat{B}\), the same optimizationt hat applied to projections applies to rejections as well:
$$ rej_{\hat{B}}\vec{A} = \vec{A} - (\vec{A} \cdot \hat{B})\hat{B} $$
Again, this should be trivial to implement:
vec Rejection(vec3 a, vec b) {
vec proj = Projection(a, b);
return Sub(a, proj);
}